数学函数中是e是什么数,等于多少(精确到

e是自然对数的底,是一个无理数,其值是7182..,它是这样定义的:当n→∞时,(1+1/n)^n的极限 注:x^y表示x的y次方。
e,作为数学常数,是自然对数函数的底数。有时称它为欧拉数(Euler number),以瑞士数学家欧拉命名;也有个较鲜见的名字纳皮尔常数,以纪念苏格兰数学家约翰纳皮尔引进对数。它就像圆周率π和虚数单位i,e是数学中最重要的常数之一。
数学中,E代表自然常数(Natural Number),用符号e表示,其数值精确到小数点后几位为718281828459045。E的命名源于苏格兰数学家约翰·纳皮尔(John Napier),他是一位17世纪的数学家,在对数理论的创立方面做出了重要贡献。
e等于多大?
〖One〗、e大概是71828。e作为数学常数,是自然对数函数的底数。有时称它为欧拉数,以瑞士数学家欧拉命名;也有个较鲜见的名字纳皮尔常数,以纪念苏格兰数学家约翰·纳皮尔引进对数。它就像圆周率π和虚数单位i,e是数学中最重要的常数之一。
〖Two〗、数学里的e是大约等于71828的一个无理数。e是数学中一个非常重要的常数,被称为自然对数的底数。它的定义是当n趋向于无穷大时,(1+1/n)的n次方的极限值。e不仅在数学中有广泛应用,还在物理学、工程学、金融学等领域发挥着重要作用。e的重要性在于它是自然对数函数的底数。
〖Three〗、e约为718281828459045。符号e为数学中一个常数,是一个无限不循环小数,且为超越数。它是自然对数函数的底数。自然常数是自然对数函数的底数,有时被称为欧拉数,也是一个无限不循环小数。也有个较鲜见的名字纳皮尔常数,以纪念苏格兰数学家约翰·纳皮尔引进对数。
〖Four〗、e是71828。e在数学中是代表一个数的符号,其实还不限于数学领域。在大自然中,建构,呈现的形状,利率或者双曲线面积及微积分教科书、伯努利家族等。现e已经被算到小数点后面两千位了。
〖Five〗、在数学中,e是极为常用的超越数之一,它通常用作自然对数的底数,即:Ln(x)=以e为底x的对数。
〖Six〗、e范围 随着n的增大,底数越来越接近1,而指数趋向无穷大,那结果趋向于71828。应用 e在数学中是代表一个数的符号,其实还不限于数学领域。在大自然中,建构呈现的形状,利率或者双曲线面积及微积分教科书、伯努利家族等都离不开e的身影。
数学中e是多少
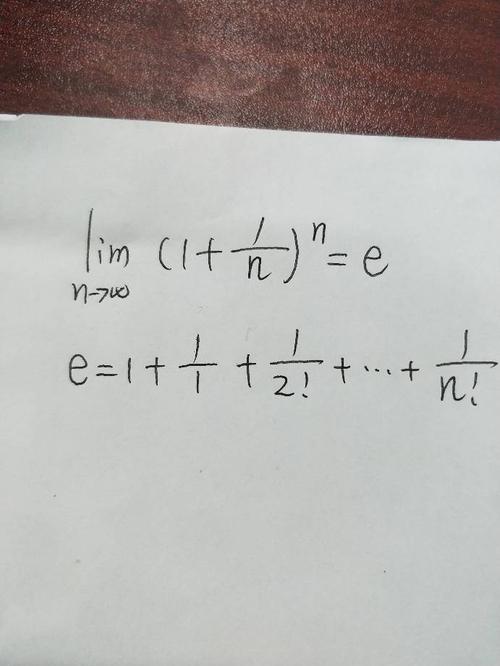
〖One〗、在数学中,e是一个超越数(大约为71828182846),它通常用作自然对数的底数。
〖Two〗、e=71828……是“自然律”的一种量的表达。“自然律”的形象表达是螺线。螺线的数学表达式通常有下面五种:(1)对数螺线;(2)阿基米德螺线;(3)连锁螺线;(4)双曲螺线;(5)回旋螺线。对数螺线在自然界中最为普遍存在,其它螺线也与对数螺线有一定的关系,不过近来我们仍未找到螺线的通式。
〖Three〗、e是自然常数,值约为718281828。自然常数是自然对数函数的底数;有时被称为欧拉数,也是一个无限不循环小数。数学中e是无理数,在数学中是代表一个数的符号,其实还不限于数学领域。在大自然中,建构,呈现的形状,利率或者双曲线面积及微积分教科书、伯努利家族等。
数学中e等于多少?
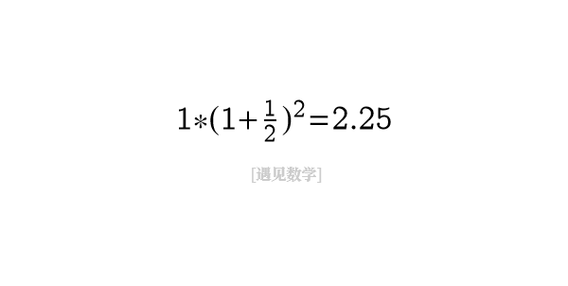
数学中e等于自然对数的底数,约等于71828。自然常数e的解释:自然常数e是一个在数学、物理等领域中广泛应用的数学常数。它是自然对数函数的底数。自然对数函数是以e为底数的对数函数,常常用于科学计算和工程应用。在自然对数函数的图像中,它与y轴交点的数值就是e的值。
数学中e等于自然对数的底数,约等于71828。解释:数学中,字母e代表的是一个特殊的常数,被称为自然对数的底数。自然对数是我们日常遇到的许多自然现象中的一种数学表达,比如利息的增长、人口的繁殖等,都呈现出一种连续复利或指数增长的模式。而这个常数的值,经过精确计算,约等于71828。
e = 71828183 自然常数,是数学中一个常数,是一个无限不循环小数,且为超越数,约为71828,就是公式为 Iim (1+1/ x ) x , x → X 或 Iim (1+z)1/ z , z →0,是一个无限不循环小数,是为超越数。在1690年,莱布尼茨在信中第一次提到常数e。
e到底在数学中是什么东西,怎么那么常用?

〖One〗、在数学中,e是一个超越数(大约为71828182846),它通常用作自然对数的底数。
〖Two〗、e,作为数学常数,是自然对数函数的底数。有时称它为欧拉数(Euler number),以瑞士数学家欧拉命名;也有个较鲜见的名字纳皮尔常数,以纪念苏格兰数学家约翰纳皮尔引进对数。它就像圆周率π和虚数单位i,e是数学中最重要的常数之一。
〖Three〗、自然对数的底数:e 是自然对数的底数,即 e^x = 10^x。自然对数的引入使得许多数学公式和计算变得更加简洁和方便。例如,求解指数函数、对数函数、三角函数等的导数和积分时,都可以直接利用自然对数的性质。 微积分中的极限:在微积分中,e 经常出现在极限的计算中。
e在数学中表示多少?怎么称这个e?
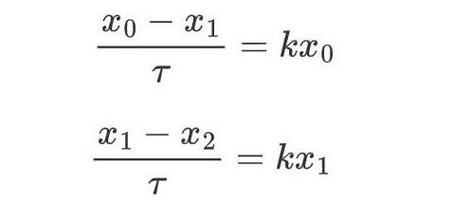
e,作为数学常数,是自然对数函数的底数。有时称它为欧拉数(Euler number),以瑞士数学家欧拉命名;也有个较鲜见的名字纳皮尔常数,以纪念苏格兰数学家约翰纳皮尔引进对数。它就像圆周率π和虚数单位i,e是数学中最重要的常数之一。
e在数学中的意思是代表自然常数,是自然数对数函数的底数,又称为欧拉数。自然常数e,一般作为数学公式中乘方数的底数或者对数的底数,是一个无限不循环的小数,值约为小数点后一百位,约为71828182845904,与圆周率π和虚数单位i一样,都是数学中最为重要的常数之一。
e代表自然常数。e是一个无限不循环小数,且为超越数,其值约为718281828459045。自然常数,符号e,为数学中一个常数。e是自然对数函数的底数。有时称e为欧拉数(Euler number),以瑞士数学家欧拉命名;也有个较鲜见的名字纳皮尔常数,以纪念苏格兰数学家约翰·纳皮尔(John Napier)引进对数。
e,作为数学常数,是自然对数函数的底数。有时称它为欧拉数(Euler number),以瑞士数学家欧拉命名;也有个较鲜见的名字纳皮尔常数,以纪念苏格兰数学家约翰·纳皮尔(John Napier)引进对数。它就像圆周率π和虚数单位i,e是数学中最重要的常数之一。
数学常数e(有时被称为欧拉数(Eulers number)或纳皮尔常数(Napiers constant)是自然对数的底数,它最早起源于经济学中的复利计算。
e可以通过以下极限定义:lim(n→∞)(1+1/n)^n。其中lim表示极限,n表示自然数。这个定义由瑞士数学家Jacob Bernoulli于1683年提出,被称为“复利计算问题”。e的性质 e是一个无理数,不能用两个整数的比值表示。e是超越数,即它不是任何有理系数多项式的根。