零点数学
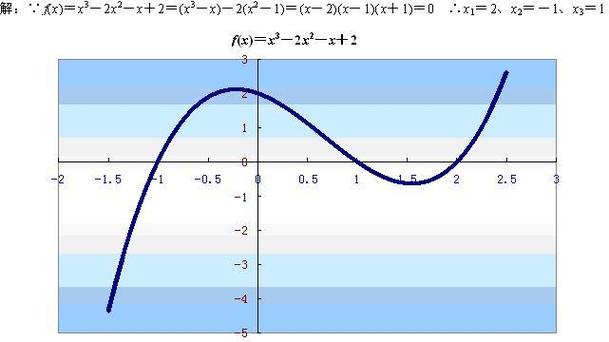
零点是对于函数y=f(x),使f(x)=0的实数x叫做函数y=f(x)的零点,即零点不是点。这样,函数y=f(x)的零点就是方程f(x)=0的实数根,也就是函数y=f(x)的图象与x轴的交点的横坐标。方程f(x)=0有实数根即函数y=f(x)的图象与x轴有交点/函数y=f(x)有零点。
在数学上,函数零点就是当f(x)=0时对应的自变量x的值,需要注意的是零点是一个数值,而不是一个点,是函数与X轴交点的横坐标。 一般地,对于函数y=f(x)(x∈R),我们把方程f(x)=0的实数根x叫作函数y=f(x)(x∈R)的零点。
一般有两种情况会这样叫,一种是函数或方程中当函数或方程等于0的时候对应的x的取值。比如有个零点存在定理,就是这个意思。还有就是指函数的导数等于0的时候对应的x的取值点。
在数学中,当我们讨论函数y=f(x),零点的概念至关重要。零点,即函数值等于零的实数x,可以理解为方程f(x)=0的实数解,或者简单地说,是函数图象与x轴交点的横坐标。换句话说,函数有零点意味着方程存在实数根,反之亦然,即函数图象与x轴有交点意味着方程有实数解。
首先,零点是数学中的基础概念之一。在数轴上,零点是原点,是正负数的分界线。在代数中,零点是方程解的一种特殊形式,它帮助我们理解方程的解集和函数的性质。在几何中,零点可以帮助我们理解空间的位置关系,如坐标系的原点。其次,零点在数学中有着重要的应用。
零点是什么意思数学

〖One〗、零点是什么意思数学如下:零点,对于函数y=f(x),使f(x)=0的实数x叫做函数y=f(x)的零点,即零点不是点。这样,函数y=f(x)的零点就是方程f(x)=0的实数根,也就是函数y=f(x)的图象与x轴的交点的横坐标。对于函数y=f(x),使f(x)=0的实数x叫做函数y=f(x)的零点,即零点不是点。
〖Two〗、一般有两种情况会这样叫,一种是函数或方程中当函数或方程等于0的时候对应的x的取值。比如有个零点存在定理,就是这个意思。还有就是指函数的导数等于0的时候对应的x的取值点。
〖Three〗、零点是指数轴上的零点,即数值为零的点。以下是详细的解释:在数学中,零点是一个数学概念。在数轴上,它可以被理解为一个具体的点,代表数字为零的点。换句话说,无论有理数或无理数,只要其值为零,都位于数轴的零点位置。零点具有独特的性质,它是正数和负数之间的分界点。
〖Four〗、零点的意思是指深夜十二点到一点,也就是0点-0点59分59秒;刻度盘的起点。零点是一个无理数,即无限不循环小数。
〖Five〗、在数学中,当我们讨论函数y=f(x),零点的概念至关重要。零点,即函数值等于零的实数x,可以理解为方程f(x)=0的实数解,或者简单地说,是函数图象与x轴交点的横坐标。换句话说,函数有零点意味着方程存在实数根,反之亦然,即函数图象与x轴有交点意味着方程有实数解。
〖Six〗、零点定义是数学中的一个基本概念,它是用来描述函数在某一特定点的行为。在更具体的术语中,零点是指函数在该点的值为0的点。这个概念在微积分、代数和许多其他数学领域中都有应用。首先,我们需要理解函数的概念。
数学零点如何判断?

图像法:对于一些无法直接求解的函数,我们可以借助图像来判断零点。首先,我们需要画出函数的图像,然后观察图像与x轴的交点。这些交点的横坐标就是函数的零点。这种方法适用于一些复杂的函数,但需要借助绘图工具,并且只能得到近似的零点。
在数学领域,函数的零点是判断的关键。当一个函数在其导数存在,并在该特定点处导数值为零时,这个点被视为函数的零点。为了判断一个函数是否含有零点,通常采用解函数方程f(x)=0的方法。此外,根据零点定理,如果函数在某一区间两端点的值正负不同,则区间内必定存在零点。
满足f(x)=0的点叫零点。例如f(x)=lnx 他的零点是x=在图像上看是函数与x轴的交点。和方程联系起来,就是f(x)=0的根。
大于0说明函数值在x轴上方。小于0说明函数值在x下方。
零点是什么意思数学如下:零点,对于函数y=f(x),使f(x)=0的实数x叫做函数y=f(x)的零点,即零点不是点。这样,函数y=f(x)的零点就是方程f(x)=0的实数根,也就是函数y=f(x)的图象与x轴的交点的横坐标。对于函数y=f(x),使f(x)=0的实数x叫做函数y=f(x)的零点,即零点不是点。
数学上把什么叫做零点

〖One〗、一般有两种情况会这样叫,一种是函数或方程中当函数或方程等于0的时候对应的x的取值。比如有个零点存在定理,就是这个意思。还有就是指函数的导数等于0的时候对应的x的取值点。
〖Two〗、在各学科中,“0”可以有不同的叫法。以下是一些常见的叫法: 数学:零、零点、零数、零值、零位。在数学中,零是一个特殊的数字,它表示没有数量或数量的开始。 物理:零点、零位。在物理中,零点通常是指温度的基准点,如摄氏度的零度或开尔文温标的绝对零度。 化学:零点、零级、零浓度。
〖Three〗、深夜十二点。 介于前一天与第二天交接时间,即是前一天的最后时刻十二点(也就是二〖Fourteen〗、时),又是第二天的开始。
在数学中,零点是什么?

〖One〗、一般有两种情况会这样叫,一种是函数或方程中当函数或方程等于0的时候对应的x的取值。比如有个零点存在定理,就是这个意思。还有就是指函数的导数等于0的时候对应的x的取值点。
〖Two〗、零点是使解析函数的值等于零的点。它在解析函数论中扮演一重要角色。单复变量的解析函数的一条重要性质是:非零解析函数的零点总是孤立的。零点是指某个函数的图像与x轴相交的点,也就是函数的解或根。在数学中,零点是一个重要的概念,它可以用来解决各种问题,如方程的求解、函数的性质分析等。
〖Three〗、在数学中,当我们讨论函数y=f(x),零点的概念至关重要。零点,即函数值等于零的实数x,可以理解为方程f(x)=0的实数解,或者简单地说,是函数图象与x轴交点的横坐标。换句话说,函数有零点意味着方程存在实数根,反之亦然,即函数图象与x轴有交点意味着方程有实数解。
在数学中,零点是什么什么
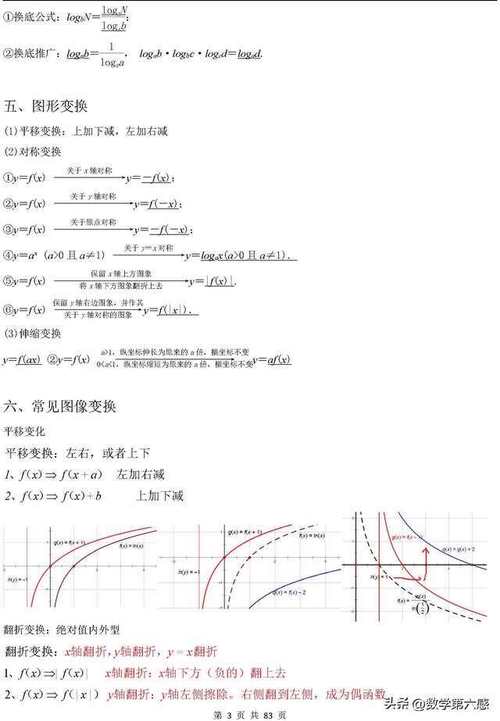
〖One〗、一般有两种情况会这样叫,一种是函数或方程中当函数或方程等于0的时候对应的x的取值。比如有个零点存在定理,就是这个意思。还有就是指函数的导数等于0的时候对应的x的取值点。
〖Two〗、零点是使解析函数的值等于零的点。它在解析函数论中扮演一重要角色。单复变量的解析函数的一条重要性质是:非零解析函数的零点总是孤立的。零点是指某个函数的图像与x轴相交的点,也就是函数的解或根。在数学中,零点是一个重要的概念,它可以用来解决各种问题,如方程的求解、函数的性质分析等。
〖Three〗、在数学中,当我们讨论函数y=f(x),零点的概念至关重要。零点,即函数值等于零的实数x,可以理解为方程f(x)=0的实数解,或者简单地说,是函数图象与x轴交点的横坐标。换句话说,函数有零点意味着方程存在实数根,反之亦然,即函数图象与x轴有交点意味着方程有实数解。
〖Four〗、首先,零点是数学中的基础概念之一。在数轴上,零点是原点,是正负数的分界线。在代数中,零点是方程解的一种特殊形式,它帮助我们理解方程的解集和函数的性质。在几何中,零点可以帮助我们理解空间的位置关系,如坐标系的原点。其次,零点在数学中有着重要的应用。
〖Five〗、在数学上,函数零点就是当f(x)=0时对应的自变量x的值,需要注意的是零点是一个数值,而不是一个点,是函数与X轴交点的横坐标。 一般地,对于函数y=f(x)(x∈R),我们把方程f(x)=0的实数根x叫作函数y=f(x)(x∈R)的零点。